La circunferencia y la recta son entonces conceptos muy fundamentales en la geometría plana. Alrededor de 300 a.C. se escribió Los elementos, un libro de gran influencia, en donde se reunió gran parte de lo que se sabía dentro de un marco común, que es la construcción con regla y compás. La fascinación griega por los problemas geométricos data de muchos años atrás. Algunos de ellos se hicieron tan famosos que ahora se llaman "clásicos" y son los siguientes:
La expresión "hallar con regla y compás" merece una aclaración: lo que se busca es una lista de instrucciones para construir lo indicado al usar solamente la regla —con la cual se puede trazar una recta por dos puntos ya conocidos— y el compás —con el cual se puede construir la circunferencia con centro dado que pasa por un punto ya conocido. Nuevos puntos sólo se obtienen como intersección de dos objetos —rectas o circunferencias— ya construidas. Para hallar la circunferencia inscrita en un triángulo dado, no se pueden dibujar una serie de circunferencias probando con diferentes centros y radios para aproximarse, poco a poco, a la solución; lo que debe indicarse es cómo se obtienen el centro y el radio para cualquier triángulo dado, no sólo uno en particular.
En Los elementos se procede paso a paso al explicar cómo resolver tareas cada vez más complicadas, pero no se resuelve ninguno de los problemas clásicos. Cada uno de estos problemas tiene una historia larga e interesante de muchos intentos fallidos. En la primera mitad del siglo XIX, se demuestra que los primeros tres de estos problemas no tienen solución, y en la segunda mitad del mismo siglo se concluye que tampoco la cuadratura del círculo tiene solución. Para ello, intervinieron matemáticos como Carl Friedrich Gauss, Evariste Galois, Pierre Wantzel y Ferdinand von Lindemann.
El adjetivo "que no tiene solución" tiene un carácter definitivo: no hay y no habrá nunca. No es que los matemáticos no han buscado lo suficientemente bien —lo hicieron por más de dos mil años y, a veces, hasta con una dedicación feroz—, sino que no puede haber solución si uno se restringe a la regla y al compás como las únicas herramientas de construcción. Desde la época de Euclides se conocen varias soluciones a los primeros tres problemas si se elimina la restricción de hacerlo sólo con regla y compás; por ejemplo, con una herramienta que traza parábolas. Con la herramienta que se muestra en la figura 4.68 se puede trisecar un ángulo con facilidad.
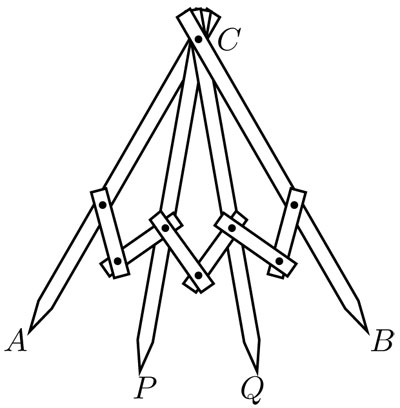
La herramienta consiste en varas y articulaciones en forma similar al compás. Para trisecar un ángulo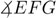 
se coloca el punto C en F y, luego, se ajustan las dos manecillas A y B sobre la recta FE y F G, respectivamente. Las puntas P y Q indican entonces la ubicación de los rayos que trisecan el ángulo dado.
La dificultad de los problemas clásicos reside en la restricción de las herramientas a, únicamente, regla y compás. En lo que sigue, daremos una idea sobre cómo es posible llegar a la conclusión de que no existe solución a los problemas clásicos. Para ello, usaremos los números complejos de la sección 4.2. Cada construcción comienza con unos datos iniciales, como una circunferencia o un triángulo dado. Empezaremos aquí con el mínimo absoluto: a partir de dos puntos dados.
